Schüler*innen-Forschungsgruppe

Ort: Raum 2.008, Mathezentrum, Endenicher Allee 60

Zeit: jeden Mittwoch um 18:00 Uhr

Leiter*innen: Dr. Regula Krapf und Dr. Henning Heller

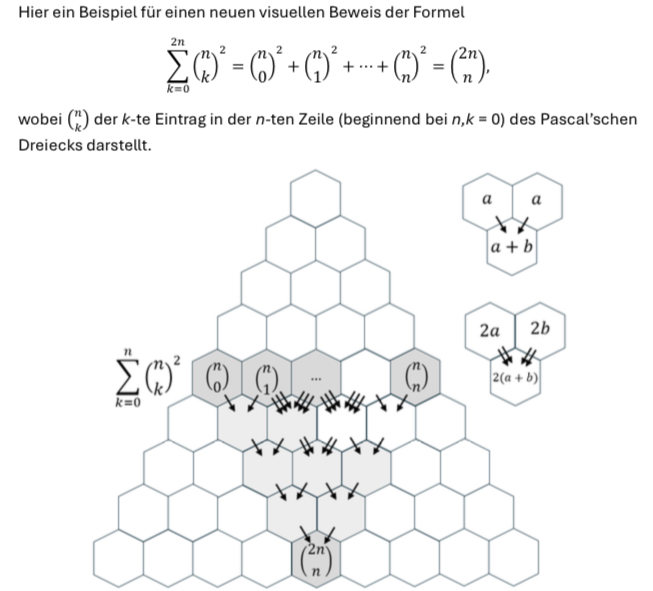
In diesem Projekt tauchten wir gemeinsam in die Welt der rekursiven Zahlenfolgen ein. Wir schauten uns Eigenschaften von Binomialkoeffizienten, Fibonacci-Zahlen, Stirling-Zahlen oder Catalan-Zahlen an und machten uns auf die Suche nach neuen, visuellen Beweisen. Dazu konstruierten wir sogenannte "Beweise ohne Worte", d.h. Beweise, die lediglich aus einem selbsterklärenden Bild bestehen. Als Werkzeug benutzten wir die Technik der "Pfeiljagd" im Pascalschen Dreieck sowie in verwandten Strukturen wie dem harmonischen Dreieck. 

An diesem Projekt haben folgende Schüler*innen  teilgenommen:

• Hannah Julia Gajdecka
• Felix Göbel
• Calum Kessler
• Lorenz Röther
• Lisa-Sophie Theemann

Hier ging es um das Thema Spiele und Spielstrategien. Als Einstieg spielten wir das Würfelspiel Regenwormen (auch bekannt als Heckmeck am Bratwurmeck), und arbeiteten uns dann in die mathematische Spieltheorie vor. 

Bei Regenwormen geht es darum, durch geschicktes Würfeln eine möglichst hohe Augensumme zu erreichen, um so unterschiedlich wertvolle Regenwurmportionen zu „angeln“. Dazu würfelt man zunächst acht identische Würfel und wählt dann alle Würfel eines Würfelsymbols (z.B. 3 Fünfen), die man beiseitelegt. Die übrigen Würfel dürfen erneut gewürfelt werden. Nach jedem erneuten Wurf müssen allerdings Symbole gewählt werden, welche man noch nicht zuvor ausgewählt hat. Es gibt mit jedem Wurf also nicht nur immer weniger Würfel, sondern auch immer weniger Symbole zur Auswahl. Sollte man gar kein Symbol mehr vorfinden, welches man noch auswählen darf, so kriegt kann man gar keine Regenwürmer und muss sogar die Portion der letzten Runde zurückgeben. 

Wann sollte man aber mit dem Würfeln aufhören? Geht man auf „Nummer Sicher“ und stoppt das Spiel früh – man bekommt dann auch eine kleinere Regenwurmportion – oder geht man das Risiko ein, alles zu verlieren? Diesen und ähnlichen Fragen sind wir in diesem Forschungsprojekt nachgegangen: 

• Finden einer optimalen Strategie für bestimmte Spielsituation
• Berechnen einer optimalen Strategie für eine einfachere Version des Spiels, z.B. mit weniger Würfeln, ohne die „Wurm-Regel“, ohne Extra-Regeln wie das „Klauen“ von Mitspielenden
• Erweitern des Spiels um weitere Regeln und Untersuchung der Auswirkungen auf die Spielstrategie
• Simulieren von Spielabläufen am Computer
• Ermitteln einer optimalen Strategie für das gesamte Spiel Regenwormen mit Computerhilfe
• Entwickeln eigener (Würfel-)Spiele, für welche sich Spielstrategien berechnen lassen
• theoretische Aspekte von (Würfel)-Spielen 

In diesem Projekt tauchen wir gemeinsam in die Welt der rekursiven Zahlenfolgen ein. Wir beginnen mit der berühmten Fibonacci-Folge. Viele Eigenschaften der Fibonacci-Zahlen kann man visuell im Hosoya-Dreieck entdecken und beweisen. Ausgehend von bekannten Mustern im Hosoya-Dreieck wollen wir neue Zahlendreiecke finden, mit denen man weitere Formeln über Fibonacci-Zahlen und andere Folgen beweisen kann. Als Werkzeug benutzen wir die Technik der ”Pfeiljagd“, mit der wir im letztjährigen Forschungsprojekt neue Muster im Pascalschen Dreieck entdeckt haben. 

Mögliche Fragestellungen für unser Forschungsprojekt sind:

(1) Welche (neuen) Muster lassen sich im Hosoya-Dreieck finden?
(2) Wie können wir neue Dreiecke basteln, in denen sich statt der Fibonacci-Zahlen andere rekursive Zahlenfolgen verstecken?
(3) Welche Formeln lassen sich in der dreidimensionalen Hosoya-Pyramide beweisen?

Nach Möglichkeit veröffentlichen wir die Ergebnisse des Forschungsprojekts. 

An diesem Projekt nehmen folgende Schüler*innen  teil:

• Calum Kessler
• Jonas Kiesel