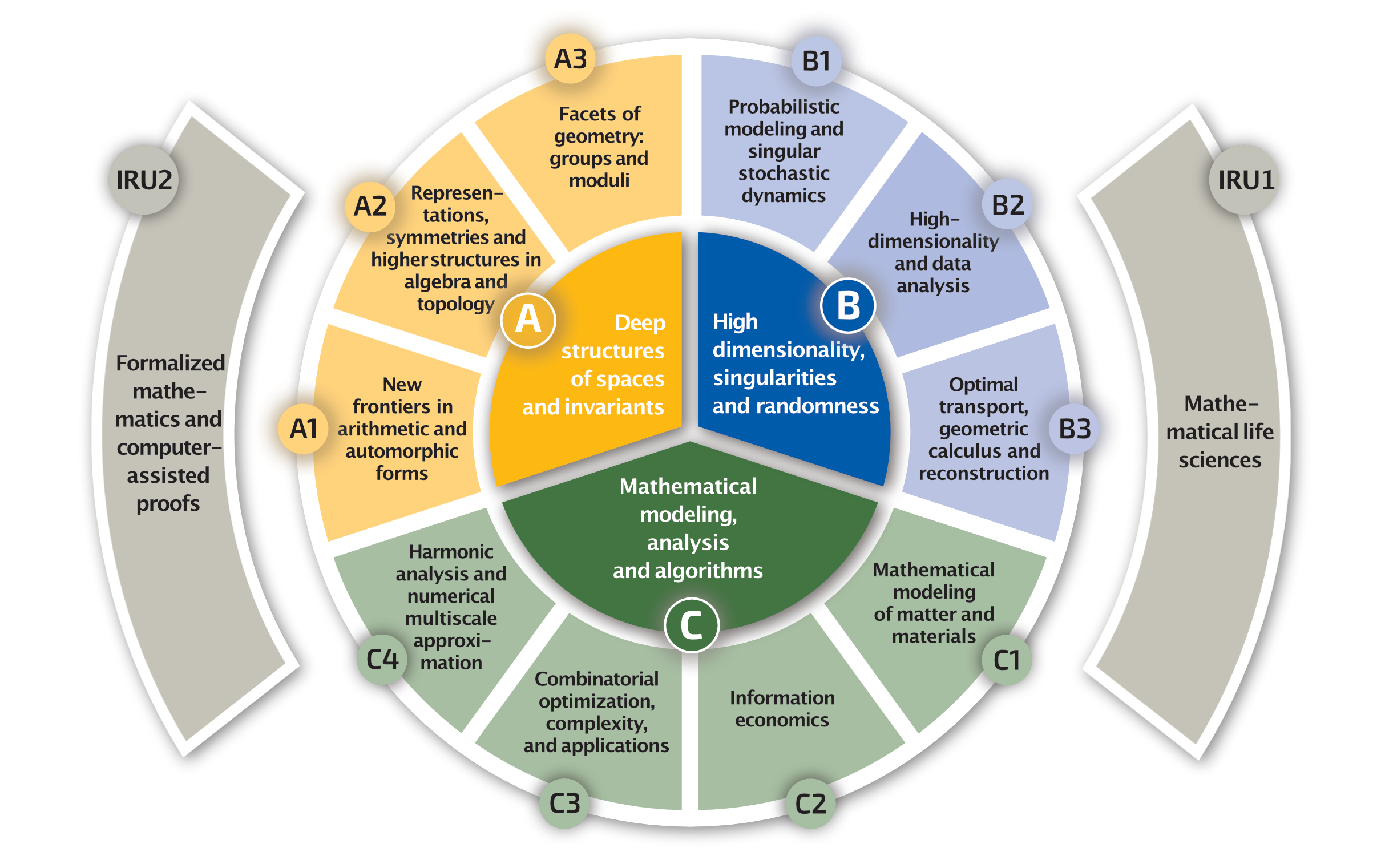
Research Areas
RA A1: New frontiers in arithmetic and automorphic forms
Valentin Blomer, Gerd Faltings, Jessica Fintzen, Dennis Gaitsgory, Daniel Huybrechts, Tasho Kaletha, Gebhard Martin, Pieter Moree, Lillian Pierce (Duke University), Michael Rapoport, Peter Scholze, Don Zagier
The Langlands program is a large web of conjectures relating, in its original setting, arithmetic and analytic questions. The local Langlands conjectures concern representations of p-adic groups, while the global Langlands conjectures combine representations for all primes p to build automorphic representations. We plan to make progress on these fundamental conjectures using a wide variety of tools, ranging from arithmetic-geometric over representation theoretic to analytic techniques.
RA A2: Representations, symmetries and higher structures in algebra and topology
Tobias Barthel, Laurent Côté, Jessica Fintzen, Dennis Gaitsgory, Markus Hausmann, Wolfgang Lück, Eveliina Peltola, Peter Scholze, Jan Schröer, Stefan Schwede, Catharina Stroppel, Geordie Williamson (University of Sydney)
This research area focuses on new theories connecting fundamental algebraic, geometric and topological methods, with the ultimate goal of understanding group actions in homotopical, geometric and algebraic contexts. Reductive groups and Hecke algebras appear in different guises. Besides common objects of study, the projects in this research area also share a key technique: the use of higher categorical methods. A prototypical example are six-functor formalisms, occurring in the Clausen–Scholze program for condensed mathematics, in Schwede’s work on global equivariant homotopy theory, in Gaitsgory–Rozenblyum’s study of derived algebraic geometry, and in Brundan–Stroppel’s formalisation of highest weight categories.
RA A3: Facets of geometry: groups and moduli
Christian Blohmann, Carl-Friedrich Bödigheimer, Laurent Côté, Philip Engel, Giles Gardam, Ursula Hamenstädt, Daniel Huybrechts, Albrecht Klemm, Matthias Kreck, Wolfgang Lück, Giacomo Mezzedimi, Werner Müller, Arunima Ray, Stephan Stadler, Karl-Theodor Sturm, Peter Teichner
Moduli spaces provide a global view of a specific mathematical landscape, often shed light on common features of particular examples, and are geometrically rich objects in themselves. We are searching for connections and shared properties of moduli spaces in different branches of mathematics. Automorphism groups arise both in the context of geometric structures as well as of their moduli spaces. Such groups can be thought of as geometric objects in their own right, but they can also be studied through their algebraic invariants, like their cohomology groups and their representations. We aim at gaining new insight in these invariants using algebraic, geometric, topological and analytic tools.
RA B1: Probabilistic modeling and singular stochastic dynamics
Sergio Albeverio, Johannes Alt, Anton Bovier, Christian Brennecke, Margherita Disertori, Andreas Eberle, Patrik Ferrari, Lorens Imhof, Muhittin Mungan, Eveliina Peltola, Sven Rady, Lisa Sauermann, Karl-Theodor Sturm
Universality and limit behavior are core themes in probabilistic modeling. This research area addresses a variety of situations where large scale limits of simple mechanisms lead to highly nontrivial structures. These include interacting particle systems, interface models, nonreversibility and memory effects in stochastic dynamics, random matrix models as well as applications to numerics, combinatorics and economics.
RA B2: High-dimensionality and data analysis
Christian Bayer, Christoph Breunig, Jürgen Dölz, Joachim Freyberger, Jochen Garcke, Michael Griebel, Alois Kneip, Dominik Liebl, Claudia Noack, Christian Rieger
Handling high-dimensional data poses significant statistical and computational challenges.This research area combines methodologies at the intersection of numerical and statistical analysis to achieve dimension reduction and to yield tractable computational procedures with valid statistical inference. The methods that we will develop are motivated by applications in econometrics, macroeconomics, biostatistics, and engineering.
RA B3: Optimal transport, geometric calculus and reconstruction
Werner Ballmann, Koen van den Dungen, Alexander Effland, Leif Kobbelt (RWTH Aachen), Andreas Kleiner, Herbert Koch, Eva Kopfer, Matthias Lesch, Benny Moldovanu, Stefan Müller, Angkana Rüland, Martin Rumpf, Karl-Theodor Sturm
Research in Area B3 addresses topical challenges in the realm of optimal transport, geometric calculus, reconstruction, and their interaction. Concepts from optimal transport play a key role in the analysis of metric measure spaces, in shape space theory, and in information design. Geometric calculus will be advanced with focus on synthetic curvature bounds, regularity estimates, and discrete–to–continuous limits. Reconstruction questions in machine learning and for inverse problems will be investigated, with strong anisotropy, dimension reduction and nonlocality as key features. The planned research will benefit from the interaction of optimal transport, geometric calculus, and reconstruction.
RA C1: Mathematical modeling of matter and materials
Sergio Conti, Margherita Disertori, Gregor Gantner, Joscha Gedicke, Jan Hamaekers, Franca Hoffmann (Caltech), Martin Lenz, Christina Lienstromberg, Stefan Müller, Ira Neitzel, Barbara Niethammer, Michael Ortiz (Bonn/Caltech), Tania Pernas-Castano, Angkana Rüland, Marc Alexander Schweitzer, Juan L. Velázquez
Material behavior is crucially influenced by a variety of microstructures on different scales. We will develop mathematical methods to understand, simulate and control the formation of microstructural patterns and their effective properties, with applications to the design of advanced materials.
RA C2: Information economics
Florian Brandl, Francesc Dilmé, Thomas Kesselheim, Andreas Kleiner, Daniel Krähmer, Stephan Lauermann, Helene Mass, Benny Moldovanu, Sven Rady, Frank Rosar, Dezsö Szalay, László Végh, Mengxi Zhang
This research area addresses open questions in information economics and mechanism design. Its aim is to produce fundamental insights into the effects of strategic information acquisition, transmission and design on the workings of market and non-market institutions for resource allocation and collective decision making. Mathematical tools applied in this RA include convex analysis, stochastic orders, optimal transport, combinatorial optimization and stochastic control.
RA C3: Combinatorial optimization, complexity, and applications
Ulrich Brenner, Anne Driemel, Jens Franke, Stephan Held, Philipp Hieronymi, Stefan Hougardy, Marek Karpinski, Thomas Kesselheim, Bernhard Korte, Kelin Luo, Dirk Müller, Petra Mutzel, Heiko Röglin, Lisa Sauermann, Vera Traub, Laura Vargas Koch, László Végh, Jens Vygen
Combinatorial optimization is ubiquitous in real-world applications and forms a cornerstone of discrete mathematics. We analyze fundamental discrete structures and devise better algorithms for linear programming and the most prominent combinatorial optimization problems, such as network design and the traveling salesman problem. We address new algorithmic challenges that arise from applications ranging from Internet economics and unsupervised learning to optimization under uncertainty. We apply our algorithms to practice via industrial cooperations, enabling innovative logistics solutions and the world’s fastest microprocessors.
RA C4: Harmonic analysis and numerical multiscale approximation
Alex Amenta, Carsten Burstedde, Jürgen Dölz, Felipe Goncalves, Michael Griebel, Herbert Koch, Lillian Piece (Duke University), Martin Rumpf, Olli Saari, Christoph Thiele, Barbara Verfürth
This research area develops a range of modern tools to theoretically analyze and numerically approximate a variety of problems with inherent multiple scales. As a common tool, we use spectral decomposition, in particular for modeling and estimates in nonlinear Fourier analysis, scattering, and surface matching. We use low rank tensor structures as a tool for representation and approximation in tailored function spaces. Multiscale approaches are employed for the investigation of scale critical phenomena, for optimal structure design, and in our construction of accurate and efficient numerical schemes.
IRU1: Mathematics and life sciences
Anton Bovier, Alexander Effland, Jan Hasenauer, Barbara Niethammer, Kevin Thurley, Juan L. Velázquez, and clinical partners
Modern life sciences build on increasingly complex and high-dimensional datasets to tackle questions ranging from basic science to clinical application. The interpretation of these datasets requires advanced mathematical tools. The focus is on the development, analysis and parametrization of models that meet the requirements of life sciences and in turn, inspire new mathematics. We build on a broad spectrum of methods, ranging from probabilistic modeling and statistics to multi-scale analysis and machine learning.
IRU2: Formalized mathematics and computer-assisted proofs
Floris van Doorn, Philipp Hieronymi, Petra Mutzel, Heiko Röglin, Christoph Thiele
Today, state of the art proof assistant software is capable of formalizing cutting-edge research within mathematics. For the upcoming funding period, HCM has established a new IRU on formalized mathematics to build on these recent advances. We will formalize brand-new research results, develop new computational tools and contribute to libraries for the rigorous formalization of mathematics. The next generation of mathematicians will be educated in finding new proofs and developing conjectures with the help and guidance of computers. The IRU will serve as a bridge between the departments of mathematics and computer science. Combined with strong existing research activities in formalized mathematics, computational complexity, decidability, and algorithmic analysis, this IRU puts Bonn in a position to significantly contribute to this rapidly developing field.
Bonn Research Chairs
The Bonn Research Chairs (BRC) program provides visiting positions for eminent scientists. The BRCs are HCM members during that time.
Bonn Research Fellows
Selected former Bonn Junior Fellows - now established professors abroad - teach and carry our research at HCM as Bonn Research Fellows (BRFs) for several weeks per year over a period of 5 years. The BRFs are HCM members during that time.
Franca
Hoffmann
