Bachelor's Program Mathematik - Profile
The Bachelor's program in Mathematics is consecutively oriented and has a research-oriented profile. It leads to an initial professional qualification and has a standard duration of study of 6 semesters (3 years), starting in the winter semester in October. A start in the summer semester in April is only possible if transferable credits have already been earned. The language of instruction is German.
From the beginning of your studies, you benefit from the mathematical breadth at the University of Bonn. The unique composition of basic lectures provides a comprehensive foundational knowledge. In the further course of study, you can choose from a wide variety of specializations in pure and applied mathematics. A secondary subject and practical trainings in the Bachelor's program offer the opportunity to apply mathematical knowledge and methods.
The courses in the Bachelor's program Mathematik are offered in the form of modules (lectures, seminars, and practical trainings). Each module lasts one semester and is completed with an examination.
Curriculum
The six compulsory lecture modules are typically completed in the first year of study. With the development of their respective specific contents, the three lectures in their combination create the basis for all mathematical theories and applications. The basic techniques of mathematical work are taught using analytical, algebraic and algorithmic methods.
-
Analysis I and II: Starting from school mathematics, differential and integral calculus is systematically developed in one and multiple dimensions. Naturally, numerous new questions and areas such as differential equations, function spaces, or differential geometry emerge.
-
Lineare Algebra I and II: The concept of the vector is abstracted, and from this, an algebraic theory of general vector spaces is formally constructed. Linear mappings on vector spaces are classified, and vector and matrix calculus are developed.
-
Algorithmische Mathematik I and II: Discrete mathematics, numerical analysis, and probability theory are mathematical areas whose application relies on the use of algorithms and computers. The lecture provides an introduction to these areas and the associated algorithms, including programming.
Starting from the third semester, introductory and advanced lectures are on the agenda. Each belongs to one of the six mathematical study areas A-F. A total of at least six lectures are required, covering four areas. For orientation, in the 3rd semester, lectures in three different areas should be attended.
From each of the 6 areas, usually one introductory (V2..) and at least one advanced lecture (V3..) are offered per semester.
For a successful completion of the degree, you must cover two areas, each with at least 18 CP, and two more with at least 9 CP from lecture modules. Therefore, you need to successfully complete two lectures from two areas and one lecture from two other areas among the six study areas.
Seminars deepen and complement the lectures. The study program requires at least one advanced seminar ("Hauptseminar"). In a seminar, each participant gives a presentation on a topic agreed upon with the lecturer beforehand. This presentation is graded as an examination performance. Seminars are intended to practice the discussion of mathematical topics, hence attendance is mandatory.
In each summer semester, several introductory seminars (S1G1) are offered. They are intended to provide an insight into the independent preparation and presentation of mathematical connections. The introductory seminars are part of the elective program.
The mandatory main seminar is usually completed in the 3rd or 4th semester. Often, it is from the area in which the bachelor thesis will be written. It is also possible to attend several (different) main seminars.
Furthermore, in the Bachelor's degree program, one of several possible practical training courses is required. The aim is to complement the theoretical and abstract study of mathematical material with practical tasks and applications, as well as to provide insight into the professional activities of mathematicians. A practical training is recommended for the 4th or 5th semester.
You can choose from:
- A practical teaching course, where you lead a tutorial group for a lecture and then reflect on your didactic activities in a portfolio.
- An external internship, where you work on a task with a mathematical focus in a company of your choice.
- A practical lab in one of the areas:
- Logic
- Discrete Mathematics
- Numerical Simulation.
A secondary subject is an integral part of the Bachelor's degree program Mathematik. The three standard secondary subjects are Physics, Computer Science and Economics. Other subjects may be possible on application. At least 24 credit points must be earned in the chosen subject. It is recommended to take a first introductory secondary subject lecture in the 2nd or 3rd semester.
- A secondary subject that differs from the three standard subjects mentioned above ("extraordinary") must be approved by the Bachelor-Master Office Mathematics before you can take examinations in it.
- In general, the rules of the teaching unit offering the module apply to all modules of your secondary subject, not those of mathematics! The registration deadlines and modalities for secondary subject modules therefore differ from subject to subject and from those of mathematics.
Further informatione under Secondary Subject, especially concerning the approval of extraordinary secondary subjects.
The degree program concludes with two compulsory modules, the Bachelor's thesis and the accompanying thesis seminar. With them you should demonstrate that you can apply scientific methods and present mathematical issues appropriately. The area of specialization for the Bachelor's thesis should ideally be chosen at the beginning of the 5th semester. The working time is 5 months.
Usually, the Bachelor's thesis begins at the end of the 5th semester. To prepare for this, it is advisable to
- attend (further) compulsory elective lectures in your chosen area of specialization,
- complete a (second) "Hauptseminar" in your area of specialization,
- contact a lecturer early enough to determine a topic for your thesis
In preparation for the Bachelor's thesis, a two-hour training on subject-specific literature research (in German) must be attended. This is a course requirement for the Bachelor's thesis seminar, which cannot be passed without this training.
The compulsive modules in the Bachelor's degree program Mathematik are
Once you have passed the compulsory lectures, there are many options to choose from. Please note our information (in German) on
The Bachelor's examination is passed as soon as the following requirements are met:
Credit Points (CP):
- The six compulsory lectures are passed.
6 · 9 = 54 CP
- Six lecture modules from areas A to F are passed, covering two different areas with two lectures each and two others with one lecture each.
6 · 9 = 54 CP
- An advances seminar ('Hauptseminar') is passed.
6 CP
- A practical training course is passed.
9 CP
- An eligible secondary subject is passed.
If more than 24 CP are earned, all excess CP count towards the elective area.
24 CP
- The Bachelor's thesis and the accompanying seminar for the Bachelor's thesis are passed.
12 + 6 = 18 CP
- Further modules from the elective area are passed. Up to 6 CP may be earned from modules of other degree programs at the University of Bonn that are not related to mathematics modules.
15 CP
- A total of 180 credit points have been obtained.
180 CP
The examination regulations contain all the legally binding regulations for your degree program. Please note the date of the examination regulations that apply to you.
The module handbook lists the modules that belong to or are permitted in your degree program. Here you will find information on the content of the modules, the admission requirements, the type and scope of the examinations and the credit points with which the module is assessed.
You can find expired examination regulations in our document archive.
Example Study Plans
The diagram shows a general study plan. The exact study plan depends on the choice of minor subject, the area of specialization, the internship and, of course, your personal motivation and aptitude. We have compiled some specific sample study plans with various parameters for you. Please note that the semester dates refer to the standard period of study. Other study plans according to individual requirements are possible, of course.
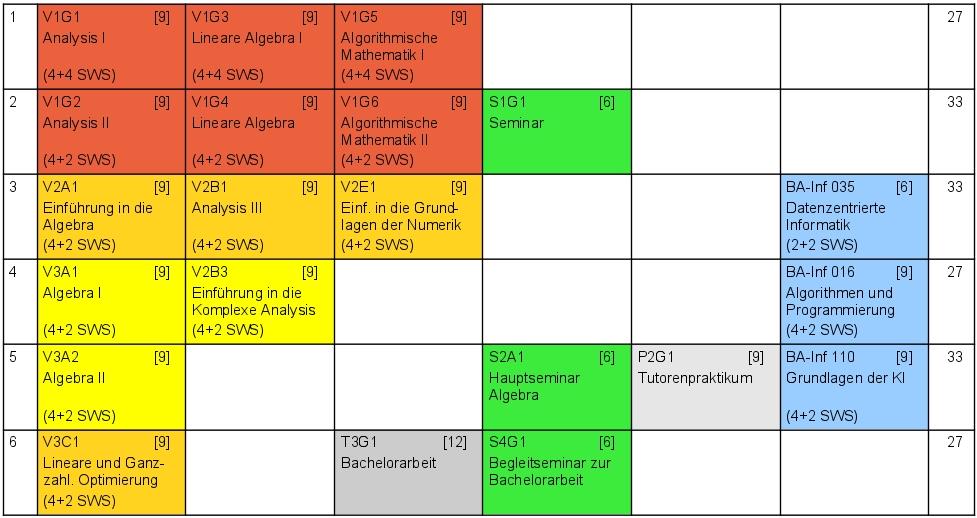
The line numbers indicate the consecutive semester count. There is no difference between the columns, but the colors have the following meanings:
- Red = Compulsory lectures
- Orange = Introductory lectures (Areas A to F)
- Yellow = Advanced lectures (Areas A to F)
- Light green / green = Seminars
- Light gray = Practical training
- Blue = Secondary subject
- Dark gray = Bachelor's thesis
The numbers in square brackets represent the number of credit points (CP), and the numbers in parentheses represent the semester hours, i.e., the weekly attendance hours.
Getting Started
- What do I need to consider when starting my studies?
- What challenges can I expect at the beginning of the degree program?
- What support options do I have for the study start?
Getting Organized
- How can I take part in a course?
- How do I register for an exam?
- Which important dates and deadlines should I not miss?
- What do I do if I am sick on the day of an exam?
Internships and Jobs
- Where can I do an internship outside the university?
- How can I prepare for starting a career?
- Where can I come into contact with employers and find possible job opportunities?
Contact Us